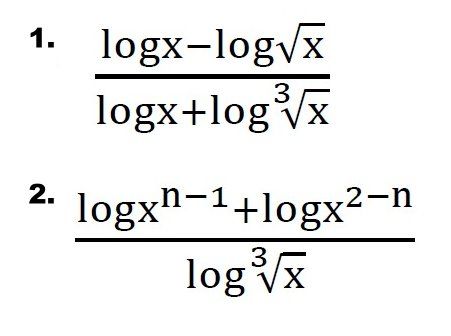
會員註冊資訊
歡迎來到香港巴士論壇。本壇是香港其中一個主要的交通討論區,亦是全港最具規模的 Der Omnibussimulator (OMSI) 討論區。請隨便瀏覽各板面,體驗討論。若有興趣加入本壇參與討論,歡迎隨時註冊帳戶,既簡單又方便。
[ 申請方法 ]
[ 申請方法 ]
F.4 Maths (Logarithm)
(t#466387)
板主: 葵芳站總站站務助理員
F.4 Maths (Logarithm)
小弟唔係幾識做以下幾題數,希望有心人可以幫幫我.. 先謝 
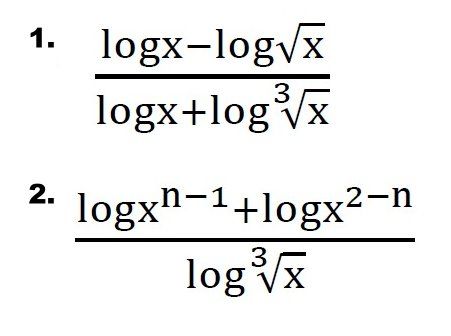
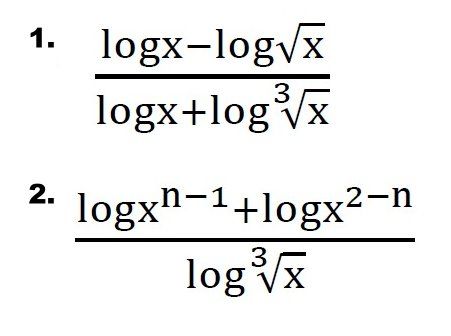

掛牌表:80K 283
♫♪ 板務小薯本地音樂流行榜 ♬♪
[2016 Week 38] 01 今生不回家 - 周國賢 | 02 沙燕之歌 - Supper Moment | 03 該死的快樂 - 王菀之
- atenulization (u#18492)
- 會員







- 文章: 3,572
- 註冊時間: 2010年7月13日 19:52:12
- 錢包: 4.30 明彩
Re: F.4 Maths (Logarithm)
記住log(x^a)=a log x
當你轉晒做log x個時,你就會計到
當你轉晒做log x個時,你就會計到
- brianlhm (u#7312)
- 會員









- 文章: 283
- 註冊時間: 2005年12月12日 14:56:11
- 錢包: 77.18 明彩
Re: F.4 Maths (Logarithm)
brianlhm :記住log(x^a)=a log x
當你轉晒做log x個時,你就會計到
我知,但係我最後都係計唔到一個整數
第一條我計到-5/6 log x...
第二條我計到6n+3...
但係兩題既答案係3/8 and 9


掛牌表:80K 283
♫♪ 板務小薯本地音樂流行榜 ♬♪
[2016 Week 38] 01 今生不回家 - 周國賢 | 02 沙燕之歌 - Supper Moment | 03 該死的快樂 - 王菀之
- atenulization (u#18492)
- 會員







- 文章: 3,572
- 註冊時間: 2010年7月13日 19:52:12
- 錢包: 4.30 明彩
- ~JY4066~JY4066~JY4066~JY4066~ (u#17273)
- 會員







- 文章: 18,883
- 註冊時間: 2009年8月25日 13:28:56
- 錢包: 2,525.78 明彩
- 來自: 59M
Re: F.4 Maths (Logarithm)
JN568@80K :brianlhm :記住log(x^a)=a log x
當你轉晒做log x個時,你就會計到
我知,但係我最後都係計唔到一個整數
第一條我計到-5/6 log x...
第二條我計到6n+3...
但係兩題既答案係3/8 and 9
不如你post你個計法出黎
睇下點解會計錯
- brianlhm (u#7312)
- 會員









- 文章: 283
- 註冊時間: 2005年12月12日 14:56:11
- 錢包: 77.18 明彩
Re: F.4 Maths (Logarithm)
JY4066 :1.
唔該哂版友
BTW你用咩software黎打?好靚~

掛牌表:80K 283
♫♪ 板務小薯本地音樂流行榜 ♬♪
[2016 Week 38] 01 今生不回家 - 周國賢 | 02 沙燕之歌 - Supper Moment | 03 該死的快樂 - 王菀之
- atenulization (u#18492)
- 會員







- 文章: 3,572
- 註冊時間: 2010年7月13日 19:52:12
- 錢包: 4.30 明彩
Re: F.4 Maths (Logarithm)
2.
=[ (n-1)log x + (2-n) log x ]/ (1/3) log x
= 3 log x / (1/3) log x
=9
=[ (n-1)log x + (2-n) log x ]/ (1/3) log x
= 3 log x / (1/3) log x
=9
- Rafael Chicharito (u#21459)
- 會員






- 文章: 117
- 註冊時間: 2011年4月5日 15:44:42
- 錢包: 0.09 明彩
- 攝影器材: NIKON D90
Re: F.4 Maths (Logarithm)
I don't think the answer of Q.2 is 9, it should be 3.
Rafael Chicharito :2.
=[ (n-1)log x + (2-n) log x ]/ (1/3) log x
= [del]3[/del] log x / (1/3) log x
=[del]9[/del]3
我 和 妳
在 幸 福 的 陽 光 下......甜 蜜 的 走
在 幸 福 的 陽 光 下......甜 蜜 的 走
- Utopia@TMS~ (u#12534)
- 會員








- 文章: 146
- 註冊時間: 2007年12月21日 14:50:08
- 錢包: 2.27 明彩
- 來自: Au--Gold
Re: F.4 Maths (Logarithm)
JN568@80K :唔該哂版友
BTW你用咩software黎打?好靚~
其實我係用Excel打 ...

第2題我同樓上一樣都係計到3,所以之前冇貼。
- ~JY4066~JY4066~JY4066~JY4066~ (u#17273)
- 會員







- 文章: 18,883
- 註冊時間: 2009年8月25日 13:28:56
- 錢包: 2,525.78 明彩
- 來自: 59M
Re: F.4 Maths (Logarithm)
Utopia@TMS~ :I don't think the answer of Q.2 is 9, it should be 3.Rafael Chicharito :2.
=[ (n-1)log x + (2-n) log x ]/ (1/3) log x
= [del]3[/del] log x / (1/3) log x
=[del]9[/del]3
師兄想問下(n-1)log x+(2-n)log x點變?
小弟唔係幾明..
thx

掛牌表:80K 283
♫♪ 板務小薯本地音樂流行榜 ♬♪
[2016 Week 38] 01 今生不回家 - 周國賢 | 02 沙燕之歌 - Supper Moment | 03 該死的快樂 - 王菀之
- atenulization (u#18492)
- 會員







- 文章: 3,572
- 註冊時間: 2010年7月13日 19:52:12
- 錢包: 4.30 明彩
Re: F.4 Maths (Logarithm)
JN568@80K :Utopia@TMS~ :I don't think the answer of Q.2 is 9, it should be 3.Rafael Chicharito :2.
=[ (n-1)log x + (2-n) log x ]/ (1/3) log x
= [del]3[/del] log x / (1/3) log x
=[del]9[/del]3
師兄想問下(n-1)log x+(2-n)log x點變?
小弟唔係幾明..
thx
舉個例:
2 log x + 3 log x
= 5 log x
所以:
(n-1)log x+(2-n)log x
= [(n-1)+(2-n)] log x
= (n-1+2-n) log x
= log x
-
本文章評分: +1
- 評分:
- ~JY4066~JY4066~JY4066~JY4066~ (u#17273)
- 會員







- 文章: 18,883
- 註冊時間: 2009年8月25日 13:28:56
- 錢包: 2,525.78 明彩
- 來自: 59M
Re: F.4 Maths (Logarithm)
JN568@80K :師兄想問下(n-1)log x+(2-n)log x點變?
Do you mean you are not sure how logx^(n-1)+logx^(2-n) can change to (n-1)log x+(2-n)log x?
Remember the rule of log: logm^n=nlogm will do. This rule is very useful.
Then you follow the steps in #11 and solve the problem.
我 和 妳
在 幸 福 的 陽 光 下......甜 蜜 的 走
在 幸 福 的 陽 光 下......甜 蜜 的 走
- Utopia@TMS~ (u#12534)
- 會員








- 文章: 146
- 註冊時間: 2007年12月21日 14:50:08
- 錢包: 2.27 明彩
- 來自: Au--Gold
Re: F.4 Maths (Logarithm)
我明點做啦~
唔該哂樓上兩位師兄幫忙
唔該哂樓上兩位師兄幫忙

掛牌表:80K 283
♫♪ 板務小薯本地音樂流行榜 ♬♪
[2016 Week 38] 01 今生不回家 - 周國賢 | 02 沙燕之歌 - Supper Moment | 03 該死的快樂 - 王菀之
- atenulization (u#18492)
- 會員







- 文章: 3,572
- 註冊時間: 2010年7月13日 19:52:12
- 錢包: 4.30 明彩
13 篇文章
• 第 1 頁 (共 1 頁)
誰在線上
正在瀏覽這個板面的使用者:沒有註冊會員 和 7 位訪客












